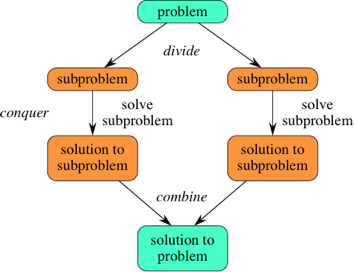
sort(a++b) can be obtained from sort(a) and sort(b). How about the Boolean function is_sorted? The value of is_sort(a++b) can not be determined merely from the return values of is_sort(a) and is_sort(b). So there must be some characteristics that tell sort and is_sort apart.Let's call a function parallelizable if it can be computed by divide and conquer. It is possible to "lift" a non-parallelizable function to a parallelizable one, such that the output of the original function can be obtained from that of the lifted function. In the above example, function
is_sort can be made parallelizable by augmenting its return value with additional information max(s) and min(s) for input list s, since $a$$+\!\!+$$b$ is sorted in ascending order if and only if $a$ and $b$ are sorted in ascending order and $\max(a)\le \min(b)$. This parallelization is also effective because it reduces the time complexity from linear to logarithmic in appropriate computation models. So here we can ask several interesting questions: 1) What functions are parallelizable? 2) Is it always possible to lift a non-parallelizable function to a parallelizable one? 3) Do parallelizable functions always have efficient parallel implementations?Homomorphism and Parallelism
After a brief survey, I found the rough ideas in my mind actually fall into a popular line of research over a long period of time. Particularly, there is a well-known result connecting homomorphisms with functions that admit divide-and-conquer imple-mentations.Definition. A function $f : [A]\rightarrow B$ is $\odot$-homomorphic for operator $\odot:B\times B\rightarrow B$ i
Note that the definition implies that $\odot$ is associative on $B$, since $+\!\!+$ is associative on $[A].$ Also, $f([\ ])$ is a unit of $\odot$ if $f$ is defined on $[\ ]$, which is a unit of $+\!\!+$ on $[A]$.
The First Homomorphism Theorem. ([1]) A function $f : [A]\rightarrow B$ can be computed by divide and conquer if and only if it is $\odot$-homomorphic for some $\odot$ on $B$.
It is clear that the $\odot$ operator captures the semantic of "combine" in a divide-and-conquer algorithm. In MapReduce, the conquer phase is done by a mapper and the combine phase by a reducer. However, as MapReduce does not specify the order of reduction, the $\odot$ operator (i.e. the reducer) has to be commutative for the outcome to be deterministic [2].
The above theorem tells us that a function is parallelizable iff it is homomorphic. Interestingly, it turns out that any non-homomorphic function can be trivially lifted to a homomorphism using a trick called "tupling". For example, this trick would lift $is\_sort: [Num]\rightarrow Bool$ to a function $is\_sort': [Num]\rightarrow [Num]\times Bool$ that is $\odot$-homomorphic
References
1. Bird, Richard S. "An introduction to the theory of lists." 1987.2. Chen, Y. F., et al. "Commutativity of Reducers." 2015.
No comments:
Post a Comment